Notes
on the use of data transformations.
Jason W. Osborne, Ph.D
North Carolina State University
| Data transformations are commonly used tools that can
serve many functions in quantitative analysis of data.
The goal of this paper is to focus on the use of three data
transformations most commonly discussed in statistics texts (square
root, log, and inverse) for improving the normality of
variables.
While these are important options for analysts, they do
fundamentally transform the nature of the variable, making the
interpretation of the results somewhat more complex.
Further, few (if any) statistical texts discuss the tremendous
influence a distribution's minimum value has on the efficacy of a
transformation. The goal of
this paper is to promote thoughtful and informed use of data
transformations. |
Data transformations are the
application of a
mathematical modification to the values of a variable.
There are a great variety of possible data transformations, from adding
constants to multiplying, squaring or raising to a power, converting to
logarithmic scales, inverting and reflecting, taking the square root of the
values, and even applying trigonometric transformations such as sine wave
transformations. The goal of this
paper is to begin a discussion of some of the issues involved in data
transformation as an aid to researchers who do not have extensive
mathematical
backgrounds, or who have not had extensive exposure to this issue before,
particularly focusing on the use of data transformation for normalization
of
variables.
Data transformation
and normality
Many statistical procedures assume that the
variables are normally
distributed. A significant violation
of the assumption of normality can seriously increase the chances of the
researcher committing either a Type I or II error (depending on the nature
of
the analysis and the non-normality). However,
Micceri (1989) points out that true normality is exceedingly rare in
education and psychology. Thus, one
reason (although not the only reason) researchers utilize data
transformations
is improving the normality of variables. Additionally,
authors such as Zimmerman (e.g., 1995, 1998) have pointed out that
non-parametric tests (where no explicit assumption of normality is made)
can
suffer as much, or more, than parametric tests when normality assumptions
are
violated, confirming the importance of normality in all statistical analyses,
not just parametric analyses.
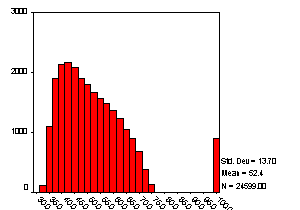 There are multiple options for dealing with
non-normal data. First, the
researcher must make certain that the non-normality is due to a valid
reason
(real observed data points). Invalid
reasons for non-normality include things such as mistakes in data entry,
and
missing data values not declared missing. Researchers
using NCES databases such as the National Education Longitudinal Survey of
1988
will often find extreme values that are intended to be missing.
In Figure 1 we see that the Composite Achievement Test scores variable
(BY2XCOMP) ranges from about 30 to about 75, but also has a group of
missing
values assigned a value of 99. If
the researcher fails to remove these the skew for this variable is 1.46,
but
with the missing values appropriately removed, skew drops to 0.35, and thus
no
further action is needed. These
are simple to remedy through correction of the value or declaration of
missing
values.
There are multiple options for dealing with
non-normal data. First, the
researcher must make certain that the non-normality is due to a valid
reason
(real observed data points). Invalid
reasons for non-normality include things such as mistakes in data entry,
and
missing data values not declared missing. Researchers
using NCES databases such as the National Education Longitudinal Survey of
1988
will often find extreme values that are intended to be missing.
In Figure 1 we see that the Composite Achievement Test scores variable
(BY2XCOMP) ranges from about 30 to about 75, but also has a group of
missing
values assigned a value of 99. If
the researcher fails to remove these the skew for this variable is 1.46,
but
with the missing values appropriately removed, skew drops to 0.35, and thus
no
further action is needed. These
are simple to remedy through correction of the value or declaration of
missing
values.
However, not all non-normality is due to data
entry error or
non-declared missing values. Two
other reasons for non-normality are the presence of outliers (scores that
are
extreme relative to the rest of the sample) and the nature of the variable
itself. There is great debate in
the literature about whether outliers should be removed or not. I am
sympathetic to Judd and McClelland's (1989) argument
that outlier removal is desirable, honest, and important. However,
not all researchers feel that way (c.f. Orr, Sackett,
and DuBois, 1991). Should a
researcher remove outliers and find substantial non-normality, or choose
not to
remove outliers, data transformation is a viable option for improving
normality
of a variable. It is beyond the
scope of this paper to fully discuss all options for data
transformation.
This paper will focus on three of the most common data transformations
utilized for improving normality discussed in texts and the
literature:
square root, logarithmic, and inverse transformations.
Readers looking for more information on data transformations might refer
to Hartwig and Dearing (1979) or Micceri (1989).
How does one
tell when a variable is violating the assumption of normality?
There are several ways to tell whether a
variable is substantially
non-normal. While researchers tend
to report favoring "eyeballing the data," or visual inspection
(Orr,
Sackett, and DuBois, 1991), researchers and reviewers often are more
comfortable
with a more objective assessment of normality, which can range from simple
examination of skew and kurtosis to examination of P-P plots (available
through
most statistical software packages) and inferential tests of normality,
such as
the Kolmorogov-Smirnov test (and adaptations of this test—researchers
wanting
more information on the K-S test and other similar tests should consult the
manual for their software as well as Goodman (1954), Lilliefors (1967),
Rosenthal (1968), and Wilcox (1997), probably in that order).
These can be useful to a researcher needing to know whether a
variable’s distribution is significantly different from a normal (or other)
distribution.
Notes on the mathematics of these data
transformations
While
many researchers in the social sciences are
well-trained in statistical methods, not many of us have had significant
mathematical training, or if we have, it has often been long
forgotten.
This section is intended to give a brief refresher on what really happens
when one applies a data transformation.
Square root transformation.
Most readers
will be familiar with this procedure-- when one applies a square root
transformation, the square root of every value is taken.
However, as one cannot take the square root of a negative number, if
there are negative values for a variable a constant must be added to move
the
minimum value of the distribution above 0, preferably to 1.00 (the
rationale for
this assertion is explained below). Another
important point is that numbers of 1.00 and above behave differently than
numbers between 0.00 and 0.99. The
square root of numbers above 1.00 always become smaller, 1.00 and 0.00
remain
constant, and numbers between 0.00 and 1.00 become larger (the square root
of 4 is 2, but the square root of 0.40 is
0.63). Thus, if you apply a square
root to a continuous variable that contains values between 0 and 1 as well
as
above 1, you are treating some numbers differently than others, which is
probably not desirable in most cases.
Log transformation(s).
Logarithmic
transformations are actually a class of transformations, rather than a
single
transformation. In brief, a
logarithm is the power (exponent) a base number must be raised to in order
to
get the original number. Any given
number can be expressed as y to the x power in an infinite number of
ways.
For example, if we were talking about base 10, 1 is 100, 100
is 102, 16 is 101.2, and so on.
Thus, log10(100)=2 and log10(16)=1.2.
However, base 10 is not the only option for log transformations.
Another common option is the Natural Logarithm, where the
constant e (2.7182818)
is the base. In
this case the natural log 100 is 4.605. As
the logarithm of any negative number or number less than 1 is undefined, if
a
variable contains values less than 1.0 a constant must be added to move the
minimum value of the distribution, preferably to 1.00.
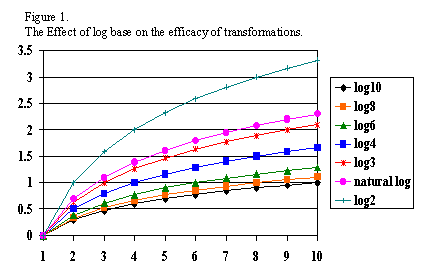
There
are good reasons to consider a range of bases
(Cleveland (1984) argues that base 10, 2, and e should always be considered at a minimum).
For example, in cases where there are extremes of range base 10 is
desirable, but when there are ranges that are less extreme, using base 10
will
result in a loss of resolution, and using a lower base (e
or 2) will serve (higher bases tend to pull extreme values in more
drastically
than lower bases). Figure 1
graphically presents the different effects of using different log
bases.
Readers are encouraged to consult Cleveland (1984).
Inverse transformation.
To take the inverse of a number (x)
is to compute 1/x. What this does is
essentially make very small numbers very large, and very large numbers very
small. This transformation has the
effect of reversing the order of your scores.
Thus, one must be careful to reflect, or reverse the distribution prior
to applying an inverse transformation. To
reflect, one multiplies a variable by -1, and then adds a constant to the
distribution to bring the minimum value back above 1.0.
Then, once the inverse transformation is complete, the ordering of the
values will be identical to the original data.
In
general, these three transformations have been presented
in the relative order of power (from weakest to most powerful).
However, it is my preference to use the minimum amount of transformation
necessary to improve normality.
Positive vs. Negative Skew.
There are, of
course, two types of skew: positive
and negative. All of the
above-mentioned transformations work by compressing the right side of the
distribution more than the left side. Thus,
they are effective on positively skewed distributions.
Should a researcher have a negatively skewed distribution, the researcher
must reflect the distribution, add a constant to bring it to 1.0, apply the
transformation, and then reflect again to restore the original order of the
variable.
Issues surrounding the use of data
transformations
Data transformations are valuable tools, with many
benefits.
However, they should be used appropriately, in an informed manner.
Too many statistical texts gloss over this issue, leaving researchers
ill-prepared to utilize these tools appropriately.
All of the transformations examined here reduce non-normality by reducing
the relative spacing of scores on the right side of the distribution more
than
the scores on the left side.
However, the very act of altering the relative
distances between data
points, which is how these transformations improve normality, raises issues
in
the interpretation of the data. If
done correctly, all data points remain in the same relative order as prior
to
transformation. This allows
researchers to continue to interpret results in terms of increasing
scores.
However, this might be undesirable if the original variables were meant
to be substantively interpretable (e.g., annual income, years of age,
grade,
GPA), as the variables become more complex to interpret due to the
curvilinear
nature of the transformations. Researchers
must therefore be careful when interpreting results based on transformed
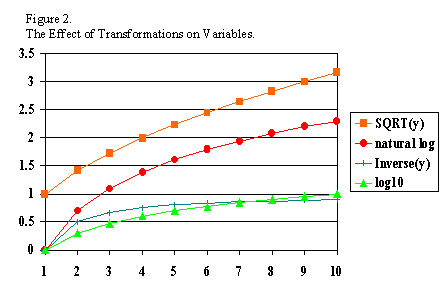
data. This issue is illustrated in Figure 2 and Table 1.
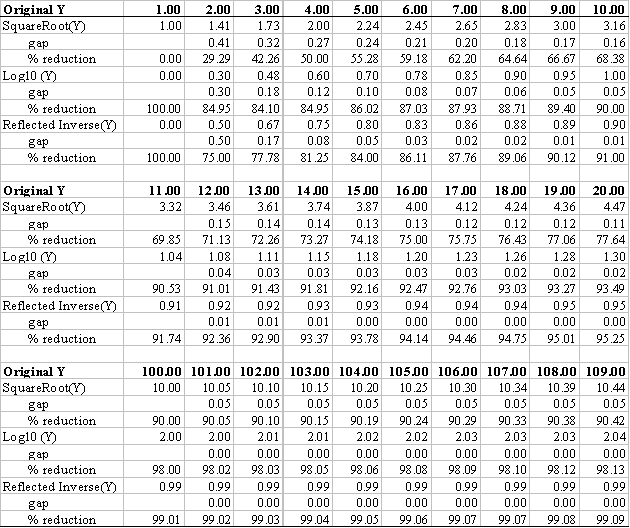
|
Table
1: Effects of various transformations on variables |
 |
While the original variable has equal spacing
between values in Figure 2 (the X axis represents the original values), the other three
lines depict the curvilinear nature of the transformations. The quality of
the transformed variable is different from the original variable.
If a variable with those qualities were subjected to a square root
transformation, where the variable's old values were {0, 1, 2, 3, 4} the
new
values are now {0, 1, 1.41, 1.73, 2}—the intervals are no longer equal
between
successive values. The examples presented in Table 1 elaborate on this
point.
It quickly becomes evident that these transformations change the relative
distance between adjacent values that were previously equidistant (assuming
interval or ratio measurement). In
the non-transformed variable, the distance between values would be an equal
1.0
distance between each increment (1, 2, 3, etc.).
However, the action of the transformations dramatically alters this equal
spacing. For example, where the
original distance between 1 and 2 had been 1.0, now it is 0.41, 0.30, or
0.50,
depending on the transformation. Further,
while the original distance between 19 and 20 had been 1.0 in the original
data,
it is now 0.11, 0.02, or 0.00, depending on the transformation.
Thus, while the order of the variable has been retained, order is all
that has been maintained. The equal
spacing of the original variable has been eliminated.
If a variable had been measured on interval or ratio scales, it has now
been reduced to ordinal (rank) data. While
this might not be an issue in some cases, there are some statistical
procedures
that assume interval or ratio measurement scales.
Does the minimum value of a distribution influence the
efficacy of a transformation?
For researchers with a strong mathematical or
statistical background,
the points made in this section are self-evident. However, over the
years many of my students and colleagues
have helped me to realize that to many researchers this point is not
self-evident; further, it is not explicitly discussed in many statistical
texts.
First, note that adding a constant to a
variable changes only the mean,
not the standard deviation or variance, skew, or kurtosis.
However, the size of the constant and the place on the number line that
the constant moves the distribution to can influence the effect of any
subsequent data transformations. As
alluded to above, it is my opinion that researchers seeking to utilize any
of
the above-mentioned data transformations should first move the distribution
so
its leftmost point (minimum value) is anchored at 1.0.
This is due to the differential effects of the
transformations across
the number line. All three
transformations will have the greatest effect if the distribution is
anchored at
1.0, and as the minimum value of the distribution moves away from 1.0 the
effectiveness of the transformation diminishes dramatically.
Recalling that these transformations improve
normality by compressing
one part of a distribution more than another, the data presented in Table 1
illustrates this point. For all
three transformations, the gap between 1 and 2 is much larger than between
9 and
10 (0.41, 0.30, and 0.50 vs. 0.16, 0.05, 0.01).
Across this range, the transformations are having an effect by
compressing the higher numbers much more than the lower numbers.
This does not hold once one moves off of 1.0, however.
If one had a distribution achored at 10 and ranging to 20, the gap
between 10 and 11 (0.15, 0.04, 0.01) is not that much different than the
gaps
between 19 and 20 (0.11, 0.02, 0.00). In
a more extreme example, the difference between 100 and 101 is almost the
same as
between 108 and 109.
In order to demonstrate the effects of minimum
values on the efficacy of
transformations, data were drawn from the National Education Longitudinal
Survey
of 1988. The variable used
represented the number of undesirable things (offered drugs, had something
stolen, threatened with violence, etc.) that had happened to a student,
which
was created by the author for another project.
This variable ranged from 0 to 6, and was highly skewed, with 40.4%
reporting none of the events occurring, 34.9% reporting only one event, and
less
than 10% reporting more than two of the events occurring.
The initial skew was 1.58, a substantial deviation from normality, making
this variable a good candidate for transformation. The relative effects of transformations on the skew of this variable are
presented in Table 2.
|
Table 2:
Variable skew as a
function of the minimum score of a distribution
|
|
|
Original
Variable
|
Min
=
1
|
Min =
2
|
Min
=
3
|
Min
=
5
|
Min
=
10
|
Min
=
100
|
|
|
|
|
|
|
|
|
|
|
Square
Root
|
1.58
|
0.93
|
1.11
|
1.21
|
1.31
|
1.42
|
1.56
|
|
Log(10)
|
1.58
|
0.44
|
0.72
|
0.88
|
1.07
|
1.27
|
1.54
|
|
Inverse
|
1.58
|
0.12
|
0.18
|
0.39
|
0.67
|
1.00
|
1.50
|
As the results indicate, all three types of
transformations worked very
well on the original distribution, anchored at a minimum of 1.
However, the efficacy of the transformation quickly diminished as
constants were added to the distribution. Even
a move to a minimum of 2 dramatically diminished the effectiveness of the
transformation. Once the minimum reached 10, the skew was over 1.0
for all
three transformations, and at a minimum of 100 the skewness was approaching
the
original, non-transformed skew in all three cases. These results
highlight the importance of the minimum value
of a distribution should a researcher intend to employ data transformations
on
that variable.
These results should also be considered when a
variable has a range of,
say 200-800, as with SAT or GRE scores where non-normality might be an
issue.
In cases where variables do not naturally have 0 as their minimum, it
might be useful to subtract a constant to move the distribution to a 0 or 1
minimum.
Conclusions
and other directions
Unfortunately, many statistical texts
provide minimal instruction
on the utilization of simple data transformations for the purpose of
improving
the normality of variables, and coverage of the use of other
transformations or
for uses other than improving normality is almost non-existent.
While seasoned statisticians or mathematicians might intuitively
understand what is discussed in this paper, many social scientists might
not be
aware of some of these issues.
The first recommendation from this paper is
that researchers always
examine and understand their data prior to
performing those long-awaited analyses. To
do less is to slight your data, and potentially draw incorrect
conclusions.
The second recommendation is to know the
requirements of the data
analysis technique to be used. As
Zimmerman (e.g., 1995, 1998) and others have pointed out, even
non-parametric
analyses, which are generally thought to be “assumption-free” can benefit
from examination of the data.
The third recommendation is to utilize data
transformations with
care—and never unless there is a clear reason.
Data transformations can alter the fundamental nature of the data, such
as changing the measurement scale from interval or ratio to ordinal, and
creating curvilinear relationships, complicating interpretation.
As discussed above, there are many valid reasons for utilizing data
transformations, including improvement of normality, variance
stabilization,
conversion of scales to interval measurement (for more on this, see the
introductory chapters of Bond and Fox (2001), particularly pages
17-19).
The fourth recommendation is that, if
transformations are to be
utilized, researchers should ensure that they anchor the variable at a
place
where the transformation will have the optimal effect (in the case of these
three, I argue that anchor point should be 1.0).
Beyond that, there
are many other issues that researchers need to familiarize themselves
with.
In particular, there are several peculiar types of variables that benefit
from attention. For example,
proportion and percentage variables (e.g., percent of students in a school
passing end-of-grade tests) and count variables of the type I presented
above
(number of events happening) tend to violate several assumptions of
analyses and
produce highly-skewed distributions. While
beyond the scope of this paper, these types of variables are becoming
increasingly common in education and the social sciences, and need to be
dealt with appropriately. The reader interested in these issues
should refer to sources such as Bartlett (1947) or Zubin (1935), or other, more
modern sources that deal with these issues, such as Hopkins (2002, available at
http://www.sportsci.org/resource/stats/index.html).
In brief, when using count variables researchers should use the square root of
the counts in the analyses, which takes care of
count data issues in most cases. Proportions
require an arcsine-root
transformation. In order to apply
this transformation, values must be between 0 and 1.
A square root of the values is taken, and the inverse sine (arcsine) of
that number is the resulting value. However,
in order to use this variable in an analysis, each observation must be
weighted by
the number in the denominator of the proportion.
References
Baker,
G. A. (1934). Transformation of
non-normal frequency distributions into normal distributions.
Annals of Mathematical Statistics, 5, 113-123.
Bond,
T. G., & Fox, C. M. (2001). Applying
the Rasch Model: Fundamental
Measurement in the Human Sciences. Mahwah,
NJ: Lawrence Erlbaum.
Bartlett,
M. S., (1947). The use of
transformation. Biometric
Bulletin, 3, 39-52.
Cleveland,
W. S. (1984). Graphical methods for
data presentation: Full scale
breaks, dot charts, and multibased logging. The
American Statistician, 38(4), 270-280.
Cohen,
J., & Cohen, P. (1983). Applied
multiple regression/correlation analysis for the behavioral
sciences.
Hillsdale, NJ: Lawrence Erlbaum Associates, Inc.
Finney,
D. J. (1948). Transformation of
frequency distributions. Nature,
London, 162, 898
Goodman, L. A. (1954). Kolmogorov-Smirnov
tests for psychological research. Psychological-Bulletin, 51,
160-168
Hopkins, W. G. (2002). A new view of
statistics. Available online at http://www.sportsci.org/resource/stats/index.html.
Lilliefors, H. W. (1968). On the Kolmogorov-Smirnov
test for normality with mean and variance unknown. Journal
of the American Statistical Association, 62, 399-402
Judd, C. M., & McClelland, G.H. (1989). Data
analysis: A model-comparison approach. San Diego, CA:
Harcourt Brace Jovanovich.
Orr,
J. M., Sackett, P. R., & DuBois, C. L. Z. (1991). Outlier
detection and treatment in I/O psychology:
A survey of researcher beliefs and an empirical illustration.
Personnel Psychology, 44,
473- 486.
Pedhazur,
E. J. (1997). Multiple regression in behavioral research.
Harcourt Brace: Orlando, FL.
Rosenthal, R. (1968). An application of the Kolmogorov-Smirnov
test for normality with estimated mean and variance. Psychological-Reports, 22, 570.
Tabachnick,
B. G., & Fidell, L. S. (2001). Using
Multivariate Statistics. New
York: Harper Collins.
Wilcox, R. R. (1997). Some practical reasons
for reconsidering the Kolmogorov-Smirnov test. British Journal of Mathematical and
Statistical Psychology, 50(1), 9-20
Zimmerman, D. W. (1995). Increasing the power of nonparametric tests by
detecting and downweighting outliers. Journal of Experimental Education, 64,
71-78.
Zimmerman,
D. W. (1998). Invalidation of
parametric and nonparametric statistical tests by concurrent violation of
two
assumptions. Journal of Experimental Education, 67, 55-68.
Zubin,
J. (1935). Note on a transformation function for proportions and
percentages. Journal
of Applied Psychology, 19, 213-220.
Author Notes
The author would like to express his gratitude to his former students at the University
of
Oklahoma for providing him with the impetus to write this paper.
Contact
information:
Jason
Osborne
ERLCE,
North Carolina State University,
Campus Box 7801
520 Poe Hall
Raleigh, NC 27695-7801
Email: jason_osborne@ncsu.edu

