Jason W. Osborne
University of Oklahoma

There are two general applications for multiple regression (MR): prediction and explanation¹. These roughly correspond to two differing goals in research: being able to make valid projections concerning an outcome for a particular individual (prediction), or attempting to understand a phenomenon by examining a variable's correlates on a group level (explanation). There has been debate as to whether these two applications of MR are grossly different, as Scriven (1959) and Anderson and Shanteau, (1977) asserts, or necessarily part and parcel of the same process (e.g., DeGroot, 1969, Kaplan, 1964; for an overview of this discussion see Pedhazur, 1997, pp. 195-198). Regardless of the philosophical issues, there are different analytic procedures involved with the two types of analyses. The goal of this paper is to present: (a) the concept of prediction via MR, (b) the assumptions underlying multiple regression analysis, (c) shrinkage, cross-validation, and double cross-validation of prediction equations, and (d) how to calculate confidence intervals around individual predictions.

What is the Difference between Using MR for Prediction versus Using MR for Explanation?

When one uses MR for explanatory purposes, that person is exploring relationships between multiple variables in a sample to shed light on a phenomenon, with a goal of generalizing this new understanding to a population. When one uses MR for prediction, one is using a sample to create a regression equation that would optimally predict a particular phenomenon within a particular population. Here the goal is to use the equation to predict outcomes for individuals not in the sample used in the analysis. Hypothetically, researchers might create a regression equation to predict twelfth-grade achievement test scores from eighth-grade variables, such as family socioeconomic status, race, sex, educational plans, parental education, GPA, and participation in school-based extracurricular activities. The goal is not to understand why students achieve at a certain level, but to create the best equation so that, for example, guidance counselors could predict future achievement scores for their students, and (hopefully) intervene with those students identified as at risk for poor performance, or to select students into programs based on their projected scores. And while theory is useful for identifying what variables should be in a prediction equation, the variables do not necessarily need to make conceptual sense. If the single greatest predictor of future achievement scores was the number of hamburgers a student eats, it should be in the prediction equation regardless of whether it makes sense (although this sort of finding might spur some explanatory research….)

How is a Prediction Equation Created?

The general process for creating a prediction equation involves gathering relevant data from a large, representative sample from the population. What constitutes "large" is open to debate, and while guidelines for general applications of regression are as small as 50 + 8*number of predictors (Tabachnick & Fidell, 1996), guidelines for prediction equations are more stringent due to the need to generalize beyond a given sample. While some authors have suggested that 15 subjects per predictor is sufficient (Park & Dudycha, 1974; Pedhazur, 1997), others have suggested minimum total sample (e.g., 400, see Pedhazur, 1997), others have suggested a minimum of 40 subjects per predictor (Cohen and Cohen, 1983; Tabachnick & Fidell, 1996). Of course, as the goal is a stable regression equation that is representative of the population regression equation, more is better. If one has good estimates of effect sizes, a power analysis might give a good estimate of the sample size. The effect of sample size on shrinkage and stability will be explored below.

Methods for entering variables into the equation. There are many ways to enter predictors into the regression equation. Several of these rely on the statistical properties of the variables to determine order of entry (e.g., forward selection, backward elimination, stepwise). Others rely on the experimenter to specify order of entry (hierarchical, blockwise), or have no order of entry (simultaneous). Current practice clearly favors analyst-controlled entry, and discourages entry based on the statistical properties of the variables as it is atheoretical. A thorough discussion of this issue is beyond the scope of this paper, so the reader is referred to Cohen and Cohen (1983) and Pedhazur (1997) for overviews of the various techniques, and to Thompson (1989) and Schafer (1991a, 1991b) for more detailed discussions of the issues.

Regardless of the method ultimately chosen by the researcher, it is critical that the researcher examine individual variables to ensure that only variables contributing significantly to the variance accounted for by the regression equation are included. Variables not accounting for significant portions of variance should be deleted from the equation, and the equation should be re-calculated. Further, researchers might want to examine excluded variables to see if their entry would significantly improve prediction (a significant increase in R-squared).

What Assumptions Must be Met When Doing a Regression Analysis?

It is absolutely critical that researchers assess whether their analyses meet the assumptions of multiple regression. These assumptions are explained in detail in places such as Pedhazur (1997) and Cohen and Cohen (1983), and as such will not be addressed further here. Failure to meet necessary assumptions can cause problems with prediction equations, often serving to either make them less generalizable than they otherwise would be, or causing underprediction (accounting for less variance than they should, such as in the case of curvilinearity or poor measurement).

How Are Prediction Equations Evaluated?

In a prediction analysis, the computer will produce a regression equation that is optimized for the sample. Because this process capitalizes on chance and error in the sample, the equation produced in one sample will not generally fare as well in another sample (i.e., R-squared in a subsequent sample using the same equation will not be as large as R-squared from original sample), a phenomenon called shrinkage. The most desirable outcome in this process is for minimal shrinkage, indicating that the prediction equation will generalize well to new samples or individuals from the population examined. While there are equations that can estimate shrinkage, the best way to estimate shrinkage, and test the prediction equation is through cross-validation or double-cross validation.

Cross-validation. To perform cross-validation, a researcher will either gather two large samples, or one very large sample which will be split into two samples via random selection procedures. The prediction equation is created in the first sample. That equation is then used to create predicted scores for the members of the second sample. The predicted scores are then correlated with the observed scores on the dependent variable (r_yy'). This is called the cross-validity coefficient. The difference between the original R-squared and r_yy'² is the shrinkage. The smaller the shrinkage, the more confidence we can have in the generalizability of the equation.

In our example of predicting twelfth-grade achievement test scores from eighth-grade variables a sample of 700 students (a subset of the larger National Education Longitudinal Survey of 1988) were randomly split into two groups. In the first group, analyses revealed that the following eighth-grade variables were significant predictors of twelfth-grade achievement: GPA, parent education level, race (white=0, nonwhite=1), and participation in school-based extracurricular activities (no=0, yes=1), producing the following equation:

Y'= -2.45+1.83(GPA) -0.77(Race) +1.03(Participation) +0.38(Parent Ed)

In the first group, this analyses produced an R-squared of .55. This equation was used in the second group to create predicted scores, and those predicted scores correlated r_yy' = .73 with observed achievement scores. With a r_yy'² of .53 (cross-validity coefficient), shrinkage was 2%, a good outcome.

Double cross-validation. In double cross-validation prediction equations are created in both samples, and then each is used to create predicted scores and cross-validity coefficients in the other sample. This procedure involves little work beyond cross-validation, and produces a more informative and rigorous test of the generalizability of the regression equation(s). Additionally, as two equations are produced, one can look at the stability of the actual regression line equations.

The following regression equation emerged from analyses of the second sample::

Y'= -4.03 +2.16(GPA) -1.90(Race) +1.43(Participation) +0.28(Parent Ed)

This analysis produced an R-squared of .60. This equation was used in the first group to create predicted scores in the first group, which correlated .73 with observed scores, for a cross-validity coefficient of .53. Note that: (a) the second analysis revealed larger shrinkage than the first, (b) the two cross-validation coefficients were identical (.53), and (c) the two regression equations are markedly different, even though the samples had large subject to predictor ratios (over 80:1).

How much shrinkage is too much shrinkage? There are no clear guidelines concerning how to evaluate shrinkage, except the general agreement that less is always better. But is 3% acceptable? What about 5%? 10%? Or should it be a proportion of the original R-squared (so that 5% shrinkage on an R-squared of .50 would be fine, but 5% shrinkage on an R-squared of .30 would not be)? There are no guidelines in the literature. However, Pedhazur has suggested that one of the advantages of double cross-validation is that one can compare the two cross-validity coefficients, and if similar, one can be fairly confident in the generalizability of the equation.

The final step. If you are satisfied with your shrinkage statistics, the final step in this sort of analysis is to combine both samples (assuming shrinkage is minimal) and create a final prediction equation based on the larger sample. In our data set, the combined sample produced the following regression line equation:

Y'= -3.23 +2.00(GPA) - 1.29(Race) +1.24(Participation) +0.32(Parent Ed)

How does sample size affect the shrinkage and stability of a prediction equation?

As discussed above, there are many different opinions as to the minimum sample size one should use in prediction research. As an illustration of the effects of different subject to predictor ratios on shrinkage and stability of a regression equation, data from the National Education Longitudinal Survey of 1988 (NELS 88, from the National Center for Educational Statistics) were used to construct prediction equations identical to our running example. This data set contains data on 24,599 eighth grade students representing 1052 schools in the United States. Further, the data can be weighted to exactly represent the population, so an accurate population estimate can be obtained for comparison. Two samples, each representing ratios of 5, 15, 40, 100, and 400 subjects per predictor were randomly selected from this sample (randomly selecting from the full sample for each new pair of a different size). Following selection of the samples, prediction equations were calculated, and double cross-validation was performed. The results are presented in Table 1.

Table 1: Comparison of double cross validation results 
with differing subject:predictor ratios

The first observation from the table is that, by comparing regression line equations, the very small samples have wildly fluctuating equations (both intercept and regression coefficients). Even the 40:1 ratio samples have impressive fluctuations in the actual equation. While the fluctuations in the 100:1 sample are fairly small in magnitude, some coefficients reverse direction, or are far off of the population regression line. As expected, it is only in the largest ratios presented, the 100:1 and 400:1 ratios, that the equations stabilize and remain close to the population equation.

Comparing variance accounted for, variance accounted for is overestimated in the equations with less than a 100:1 ratio. Cross-validity coefficients vary a great deal across samples until a 40:1 ratio is reached, where they appear to stabilize. Finally, it appears that shrinkage appears to minimize as a 40:1 ratio is reached. If one takes Pedhazur's suggestion to compare cross-validity coefficients to determine if your equation is stable, from these data one would need a 40:1 ratio or better before that criterion would be reached. If the goal is to get an accurate, stable estimate of the population regression equation (which it should be if that equation is going to be widely used outside the original sample), it appears desirable to have at least 100 subjects per predictor.

Calculating a Predicted Score, and Confidence Intervals Around That Score

There are two categories of predicted scores relevant here: scores predicted for the original sample, and scores that can be predicted for individuals outside the original sample. Individual predicted scores and confidence intervals for the original sample are available in the output available from most common statistical packages. Thus, the latter will be addressed here.

Once an analysis is completed and the final regression line equation is formed, it is possible to create predictions for individuals who were not part of the original sample that generated the regression line (one of the attractive features of regression). Calculating a new score based on an existing regression line is a simple matter of substitution and algebra. However, no such prediction should be presented without confidence intervals. The only practical way to do this is through the following formula:

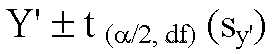
where s_y' is calculated as: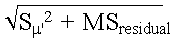

where 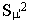is the squared standard error of mean predicted scores (standard error of the estimate, squared), and the mean square residual, both of which can be obtained from typical regression output.²

Summary and suggestions for further study

Multiple regression can be an effective tool for creating prediction equations providing adequate measurement, large enough samples, assumptions of MR are met, and care is taken to evaluate the regression equations for generalizability (shrinkage). Researchers interested in this topic might want to explore the following topics: (a) the use of logistic regression for predicting binomial or discrete outcomes, (b) the use of estimation procedures other than ordinary least squares regression that can produce better prediction (e.g., Bayesian estimation, see e.g. Bryk and Raudenbush, 1992), and (c) alternatives to MR when assumptions are not met, or when sample sizes are inadequate to produce stable estimates, such as ridge regression (for an introduction to these alternative procedures see e.g., Cohen & Cohen, 1983, pp.113-115). Finally, if researchers have nested or multilevel data, they should use multilevel modeling procedures (e.g., HLM, see Bryk & Raudenbush, 1992) to produce prediction equations.

SUGGESTED READING:

Anderson, N. H., & Shanteau, J. (1977). Weak inference with linear models. Psychological Bulletin, 84, 1155-1170.

Bryk, A.S., & Raudenbush, S. W. (1992). Hierarchical linear models: Applications and data analysis methods. Newbury Park, CA: Sage Publications.

Cohen, J., & Cohen, P. (1983). Applied multiple regression/correlation analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc.

DeGroot, A. D. (1969). Methodology: Foundations of inference and research in the behavioral sciences. The Hague: Mouton.

Kaplan, A. (1964). The conduct of inquiry: Methodology for behavioral science. San Francisco: Chandler.

Park, C., & Dudycha, A. (1974). A cross-validation approach to sample size determination. Journal of the American Statistical Association, 69, 214-218.

Pedhazur, E. J. (1997). Multiple regression in behavioral research. Harcourt Brace: Orlando, FL.

Scriven, M. (1959). Explanation and prediction in evolutionary theory. Science, 130, 477-482.

Thompson, B. (1989). Why won't stepwise methods die? Measurement and Evaluation in Counseling and Development, 21, 146-148.

Schafer, W. D. (1991a). Reporting hierarchical regression results. Measurement and Evaluation in Counseling and Development, 24, 98-100.

Schafer, W.D. (1991b). Reporting nonhierarchical regression results. Measurement and Evaluation in Counseling and Development, 24, 146-149.

Tabachnick, B. G., & Fidell, L. S. (1996). Using Multivariate Statistics. New York: Harper Collins.

FOOTNOTES

1. Some readers may be uncomfortable with the term "explanation" when referring to multiple regression, as these data are often correlational in nature, while the term explanation often implies causal inference. However, explanation will be used in this article because: (a) it is the convention in the field, (b) here we are talking of regression with the goal of explanation, and (c) one can come to understanding of phenomena by understanding associations without positing or testing strict causal orderings..

2. It is often the case that one will want to use standard error of the predicted score when calculating an individual confidence interval. However, as that statistic is only available from statistical program output, and only for individuals in the original data set, it is of limited value for this discussion. Here we suggest using the standard error of the mean predicted scores, as it is the best estimate of the standard error of the predicted score, knowing it is not completely ideal, but lacking any other alternative.

AUTHOR NOTES

Correspondence relating to this article can be addressed to Jason W. Osborne, Department of Educational Psychology, University of Oklahoma, 820 Van Vleet Oval, Norman, OK, 73019, or via email at josborne@ou.edu. Special thanks go to William Schafer, whose many good suggestions and critical eye helped to substantially shape this paper.

Sitemap 1 - Sitemap 2 - Sitemap 3 - Sitemap 4 - Sitemape 5 - Sitemap 6