J. Thomas Kellow, University of Houston
Victor L. Willson, Texas A&M University

Walt Haney’s (2000) treatise on The Myth of the Texas Miracle in Education highlights a number of concerns related to high-stakes decision-making in K-12 settings.  His elaboration of the history and development of the Texas Assessment of Academic Skills (TAAS) was illuminating, especially for those unfamiliar with the often capricious fashion in which standards are ultimately set for high-stakes decisions.  The evidence Haney presents in evaluating the TAAS fits well with Samuel Messick’s (1994) argument for considering the consequences of test use.  Although sometimes referred to as consequential validity, Messick considered this aspect of test interpretation and use to be one of many forms of construct validity.  His view of the evaluative role of validity is summarized nicely in the following paragraph:

When assessing any of these constructs – whether attributes of persons or groups, of objects or situations – validity needs to be systematically addressed, as do other basic measurement issues such as reliability, comparability, and fairness.  This is so because validity, comparability, and fairness are not just measurement principles, they are social values that have meaning and force outside of measurement whenever evaluative judgment and decisions are made.  As such, validity assumes both a scientific and political role that can by no means be fulfilled by a simple correlation coefficient between test scores and a purported criterion or by expert judgments that test content is relevant to the proposed test use (p. 1).

One technical aspect of the TAAS that Haney takes to task is the reliability of scores yielded by the test and the potential for misclassification as a function of measurement error.  As the author notes, “The reason the setting of passing scores on a high-stakes test such as the TAAS is so important is that the passing score divides a continuum of scores into just two categories, pass and fail.  Doing so is hazardous because all standardized test scores contain some degree of measurement error”  (Haney 2000, p. 10).  Haney also points out that measures of test-retest (or alternate-form) reliability and not internal consistency should ideally be used to inform judgment as to the potential for misclassfication due to measurement error.  In light of the conspicuous absence of test-retest data on the TAAS, he attempts to use extant data to approximate this reliability estimate as compared to the internal consistency (KR20) estimates provided by the Texas Education Agency (TEA).  Although the approach he uses is somewhat problematic (see Wainer, 1999), it is clear that these test-retest estimates are lower than the KR20 estimates.

The thrust of Haney’s argument is that measurement error inherent in the TAAS (or any other measure, for that matter) contributes appreciably to the rate of “false negatives,” or misclassifying passing students as non-passing.  His focus, however, is exclusively on the tenth-grade Exit-Level TAAS since this is the test high school students in the state of Texas must pass in order to graduate from high school (although it is not the sole criterion).  But in some districts, the TAAS is also being used at other grade levels for high-stakes decisions – namely, promotion and retention of students.  Waco Independent School District and Houston Independent School District, among others, require students in grades 3 through 8 to pass all portions of the TAAS in order to be considered for promotion to grade level.  Students who fail any subtest during the statewide spring administration can expect to attend mandatory summer school, after which they are tested on a “released” version of the TAAS.  Those students who fail are held back in grade.  This stands in contrast to the Exit-Level testing schedule where, as Haney notes, students have as many as eight opportunities to pass the exam.  In addition, the TEA has announced plans to use the TAAS for promotion/retention decisions in the third, fifth, and eighth grades beginning in the fall of 2001 (Texas Education Agency, 1999).

Given the current political climate and the clarion calls for school district accountability throughout the nation, the number of districts in Texas using the TAAS for promotion and retention decisions in all tested grades no doubt will increase.  Indeed, the Houston model has been lauded for its strict criteria for student grade promotion, which is believed to increase student motivation and achievement while reducing the student dropout rate (Markley, 1999).  Our purpose in this response is to elaborate on the potential social consequences of using the TAAS for high-stakes decisions, specifically grade promotion and retention.  The question we asked is rather simple:  “Given the imperfect reliability of the TAAS test, how many students with a true passing score are potentially misclassified as failing across grades and subtests in a given year”?   Fortunately, sufficient summary statistics and frequency distributions were available from the TEA to estimate these numbers. 

The most recent reliability estimates for the TAAS were reported for the 1998-99 school year; therefore we used means, standard deviations, and frequency distributions for this same year.  We want to emphasize that there are a number of ways to go about this estimation process. The method presented emerged because it is fairly intuitive and required minimal summary statistics from the data. 

First, we should note that the 70% passing standard on the TAAS mentioned by Haney is not fixed across grades and subtests.  Because of differential item and thus test difficulty, the proportion of items correct needed to pass a given subtest ranges from .64 to .75, according to the TEA.  The Texas Learning Index (TLI) was developed by the TEA for the purpose of, among other things, providing a consistent passing standard across test forms.  The TLI is a linear standardized scoring transformation with a standard deviation of 15  and an anchor (rather than mean) of 70, which represents the passing standard for a given subtest at a given grade.  The TLI is calculated in z-score form as:

Although the TLI observed score of 70 is the passing standard, this standard fails to incorporate measurement error in determining the appropriate cut score.  Specifically, the process of modifying cut-scores involves determining the domain score in proportion-correct form that constitutes mastery (t_o ) and then adjusting this value to estimate a new cut score (X₀) in number-correct form that reflects the measurement error in the test data (Crocker & Algina, 1986).  Huynh and Sanders (1980) provide an approximate procedure for this purpose that works well when a test consists of 20 or more items and the observed proportion correct cut score falls within .50 to .80. The TAAS subtests meet both criteria.  This formula is given as:

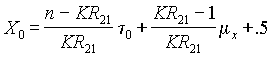(2)

Where n is the number of items on the test, t_o is the observed proportion-correct cut score, and m_x is the mean number of items correct.  As noted by Crocker and Algina (1986), as KR21 approaches 1.0, X₀  approaches n t_o + .5 irrespective of the value of m_x. 

Our question focuses on the estimate X₀  when transformed to a TLI score metric.  Put simply: What is the passing TLI adjusted for measurement error for a given subtest in a given grade, and what percent and number of students met this adjusted criterion but not the standard cut score of 70?  The following steps were employed to determine X₀ in TLI form:

1. calculate X₀ in raw score form;

2. transform X₀ into a z-score;

3. substitute z X₀ for z observed in Formula 1.

We then used TLI frequency distributions for the 1998-99 administration of the TAAS to determine the percent and number of students who received a TLI score of X₀  or higher but less that 70.  Because the TLI frequency distribution tables obtained from TEA report whole number values, we rounded the obtained X₀ estimates to the closest whole number.  These data are presented in Table 2 disaggregated by subtest and grade.

Because of the rounding procedure mentioned earlier, these percentages and student numbers are approximations.  Roughly 35,182 students who took the reading subtest in the 1998-99 school year were classified as failing, despite having an observed score that would have met (or exceeded) the passing criterion had the presence of measurement error been incorporated into the cut score.  On the mathematics subtest, 43,077 students who failed met (or exceeded) the adjusted observed criterion score. 

     Because all tests are inherently unreliable to some degree, measurement errors must be accommodated in the development of cut-scores for criterion-referenced tests, particularly when these instruments are used to make high-stakes decisions for student placement.  Our analysis focused exclusively on the impact of false negative classification errors.  There exists, of course, a second type of misclassification termed a “false positive,” or misclassifying non-passing students as passing.  Although both types of misclassification are serious, a survey of Texas educators conducted by Haney (2000) as part of his investigation of the TAAS  indicated that respondents viewed the consequences of denying a high school diploma to a qualified student based on a classification error (false negative) as considerably more serious that granting a diploma to an unqualified student (false positive).  Indeed, only the consequences to society of granting a license to an unqualified pilot, physician, or teacher, respectively, were viewed as more serious.  Additionally, the literature on grade retention is fairly consistent in noting the deleterious effects of these policies (e.g., increased dropout rates), particularly when strong individualized remediation procedures are not in place (McCoy & Reynolds, 1999).  Put simply, based on Haney’s (2000) survey and the empirical findings on the consequences of retaining students, we feel it seems reasonable to place greater emphasis on the occurrence of false negatives -- at least in the context of education and student promotion decisions.

     The estimation process we employed produced results suggesting that about 2% of students who take the state-mandated TAAS exam will be scored as false negatives on one or more of the subtests.  The consequences of misclassification will become more evident as the TAAS is increasingly used for promotion and retention decisions in Texas.  There is, however, a much larger picture emerging at the national level regarding the (mis)use of standardized assessment tools.  To put this in a broader perspective, we extended our analysis to include an estimate of how many students nationally would be misclassified as false negatives if a testing program such as the TAAS were in place.  We assumed that testing would include the same grade levels as the Texas accountability model, and assumed also a national testing instrument with the same technical adequacy (reliability) as the TAAS.  National data were obtained for the 1998-99 school year disaggregated by grade level.   Combining both reading and mathematics error rates results in approximately  1.1 million students that would potentially be misclassified as false negatives each year across the country.  Two percent clearly is no small number in the national context.        

     The recently installed Bush administration has issued school accountability reform measures that rely almost exclusively on standardized achievement tests.  Many questions remain, however, regarding the structure and implementation of the testing program that will serve as a measure of student performance across states.  What these tests will look like, the extent to which they yield scores that are psychometrically meaningful, and the importance of the scores in guiding student-level decisions are issues that have not been addressed to date.   It is notable that both the American Psychological Association (APA) and, more recently, the American Educational Research Association (AERA) have issued position statements advising against the use of a single assessment for high-stakes decisions at the individual level.  It seems probable, however, that the national appetite for school accountability in the form of student achievement scores will overwhelm any concerns over the ethical consequences of high-stakes testing.

Haney, W. (2000).   The myth of the Texas Miracle in education.  Education Policy Analysis Archives [On-line serial], 8 (41).  Available:  http://epaa.asu.edu/epaa/v8n41/.

Markley, M.  . (1999, September 8). HISD rules holding more students back:  Expanded standards cut social promotions.  Houston Chronicle, p. A1.

Messick, S. A.  (1994).  Foundations of validity:  Meaning and consequences in psychological assessment.  European Journal of Psychological Assessment, 10, 1-9.

McCoy, A. R., & Reynolds, A. J.  (1999).  Grade retention and school performance:  An extended investigation.  Journal of School Psychology, 37, 273-298.

Texas Education Agency (1999, June 22).  Briefing book:  Legislation affecting public education [On-line].  Available:  http://www.tea.state.tx.us/brief/doc2.html.

Wainer, H. (1999).   Comments on the ad hoc committee’s critique of the Massachusetts Teacher Tests.   Education Policy Analysis Archives [On-line serial], 7 (5).  Available:  http://epaa.asu.edu/epaa/v7n5.html.