|
Osborne, Jason W. (2003). Effect sizes and the disattenuation of correlation and regression coefficients: lessons from educational psychology. Practical Assessment, Research & Evaluation, 8(11). Retrieved August 18, 2006 from http://edresearch.org/pare/getvn.asp?v=8&n=11 . This paper has been viewed 580 times since 5/27/03.
Effect
Sizes and the Disattenuation of Correlation and Regression Coefficients: Lessons
from Educational Psychology.
Jason W. Osborne
North Carolina
State
University
| This
paper presents an overview of the concept of disattenuation of correlation and
multiple regression coefficients, some discussion of the pros and cons of this
approach, and illustrates the effect of performing this procedure using data
from a large survey of Educational Psychology research. |
The
nature of social science research means that many variables we are interested
in are also difficult to measure, making measurement error a particular
concern. In simple correlation and regression, unreliable measurement causes
relationships to be under-estimated increasing the risk of Type II
errors. In the case of multiple regression or partial correlation, effect
sizes of other variables can be over-estimated if the covariate is not
reliably measured, as the full effect of the covariate(s) would not be
removed.
In
both cases this is a significant concern if the goal of research is to
accurately model the “real” relationships evident in the population. Although
most authors assume that reliability estimates (Cronbach alphas) of .70 and
above are acceptable (e.g., Nunnally, 1978) and Osborne, Christensen, and
Gunter (2001) reported that the average alpha reported in top Educational
Psychology journals was .83, measurement of this quality still contains enough
measurement error to make correction worthwhile, as illustrated below.
Correction
for low reliability is simple, and widely disseminated in most texts on
regression, but rarely seen in the literature. I argue that authors should
correct for low reliability to obtain a more accurate picture of the “true”
relationship in the population, and, in the case of multiple regression or
partial correlation, to avoid over-estimating the effect of another variable.
Reliability and simple
regression
Since
“the presence of measurement errors in behavioral research is the rule rather
than the exception” and the “reliabilities of many measures used in the
behavioral sciences are, at best, moderate” (Pedhazur, 1997, p. 172) it is
important that researchers be aware of accepted methods of dealing with this
issue. For simple correlation, Equation #1 provides an estimate of the “true”
relationship between the IV and DV in the population:
|
 |
(1) |
In this equation, r12
is the observed correlation, and r11 and r22
are the reliability estimates of the variables. There are examples of the
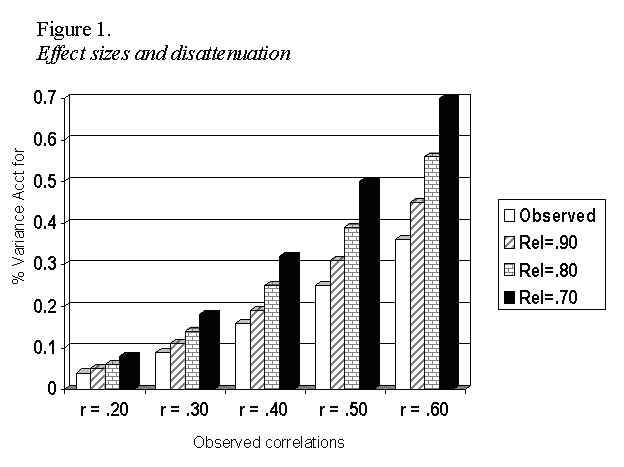
effects of disattenuation in Table 1. For example, even when reliability is
.80, correction for attenuation substantially changes the effect size
(increasing variance accounted for by about 50%). When reliability drops to
.70 or below this correction yields a substantially different picture of the
“true” nature of the relationship, and potentially avoids Type II errors.
|
Table
1: Example
Disattenuation of Correlation Coefficients
|
|
|
Correlation Coefficient
|
|
Reliability
estimate:
|
0.10 (.01)
|
0.20 (.04)
|
0.30 (.09)
|
0.40 (.16)
|
0.50 (.25)
|
0.60 (.36)
|
|
0.95
|
0.11 (.01)
|
0.21 (.04)
|
0.32 (.10)
|
0.42 (.18)
|
0.53 (.28)
|
0.63 (.40)
|
|
0.90
|
0.11 (.01)
|
0.22 (.05)
|
0.33 (.11)
|
0.44 (.19)
|
0.56 (.31)
|
0.67 (.45)
|
|
0.85
|
0.12 (.01)
|
0.24 (.06)
|
0.35 (.12)
|
0.47 (.22)
|
0.59 (.35)
|
0.71 (.50)
|
|
0.80
|
0.13 (.02)
|
0.25 (.06)
|
0.38 (.14)
|
0.50 (.25)
|
0.63 (.39)
|
0.75 (.56)
|
|
0.75
|
0.13 (.02)
|
0.27 (.07)
|
0.40 (.16)
|
0.53 (.28)
|
0.67 (.45)
|
0.80 (.64)
|
|
0.70
|
0.14 (.02)
|
0.29 (.08)
|
0.43 (.18)
|
0.57 (.32)
|
0.71 (.50)
|
0.86 (.74)
|
|
0.65
|
0.15 (.02)
|
0.31 (.10)
|
0.46 (.21)
|
0.62 (.38)
|
0.77 (.59)
|
0.92 (.85)
|
|
0.60
|
0.17 (.03)
|
0.33 (.11)
|
0.50 (.25)
|
0.67 (.45)
|
0.83 (.69)
|
---
|
|
Note: Reliability estimates for this example assume the
same reliability for both variables. Percent variance accounted for (shared
variance) is in parentheses. |
Reliability and Partial
Correlations
With
each independent variable added to the regression equation, the effects of less
than perfect reliability on the strength of the relationship becomes more
complex and the results of the analysis more questionable. With the addition
of one independent variable with less than perfect reliability each succeeding
variable entered has the opportunity to claim part of the error variance left
over by the unreliable variable(s). The apportionment of the explained
variance among the independent variables will thus be incorrect. The more
independent variables added to the equation with low levels of reliability the
greater the likelihood that the variance accounted for is not apportioned
correctly. This can lead to erroneous findings and increased potential for
Type II errors for the variables with poor reliability, and Type I errors for
the other variables in the equation. Obviously, this gets increasingly complex
as the number of variables in the equation grows.
A simple example, drawing
heavily from Pedhazur (1997), is a case where one is attempting to assess the
relationship between two variables controlling for a third variable (r12.3).
When one is correcting for low reliability in all three variables Equation #2
is used, Where r11, r22, and r33 are
reliabilities, and r12, r23, and r13 are
relationships between variables. If one is only correcting for low reliability
in the covariate one could use Equation #3.
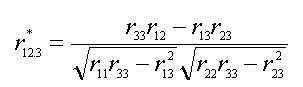 |
(2) |
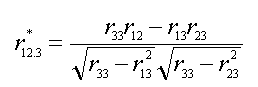 |
(3) |
Table 2 presents some examples
of corrections for low reliability in the covariate (only) and in all three
variables. Table 2 shows some of the many possible combinations of
reliabilities, correlations, and the effects of correcting for only the
covariate or all variables. Some points of interest: (a) as in Table 1, even
small correlations see substantial effect size (r 2) changes when
corrected for low reliability, in this case often toward reduced effect sizes
(b) in some cases the corrected correlation is not only substantially different
in magnitude, but also in direction of the relationship, and (c) as expected,
the most dramatic changes occur when the covariate has a substantial
relationship with the other variables.
|
Table
2: Values
of r12.3 and r212.3 after
correction low reliability
|
|
|
|
Reliability of Covariate
|
|
Reliability of All
Variables
|
|
Examples:
|
.80
|
.70
|
.60
|
|
.80
|
.70
|
.60
|
|
r12
|
r13
|
r23
|
Observed r12.3
|
r12.3
|
r12.3
|
r12.3
|
|
r12.3
|
r12.3
|
r12.3
|
|
.3
|
.3
|
.3
|
.23
|
.21
|
.20
|
.18
|
|
.27
|
.30
|
.33
|
|
.5
|
.5
|
.5
|
.33
|
.27
|
.22
|
.14
|
|
.38
|
.42
|
.45
|
|
.7
|
.7
|
.7
|
.41
|
.23
|
.00
|
-.64
|
|
.47
|
.00
|
-
|
|
.7
|
.3
|
.3
|
.67
|
.66
|
.65
|
.64
|
|
.85
|
.99
|
-
|
|
.3
|
.5
|
.5
|
.07
|
-.02
|
-.09
|
-.20
|
|
-.03
|
-.17
|
-.64
|
|
.5
|
.1
|
.7
|
.61
|
.66
|
.74
|
.90
|
|
-
|
-
|
-
|
| Note: In some examples we would produce impossible values
that we do not report. |
Reliability and Multiple Regression
Research
by Bohrnstedt (1983) has argued that regression coefficients are primarily
affected by reliability in the independent variable (except for the intercept,
which is affected by reliability of both variables), while true correlations
are affected by reliability in both variables. Thus, researchers wanting to
correct multiple regression coefficients for reliability can use Formula 4,
which is presented in Bohrnstedt (1983), and which takes this issue into
account:
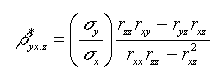 |
(4) |
Some examples of
disattenuating multiple regression coefficients are presented in Table 3. In these examples (which admittedly are a very
narrow subset of the total possibilities), corrections resulting in impossible
values were rare, even with strong relationships between the variables, and
even when reliability
|
Table
3: Example
Disattenuation of Multiple Regression Coefficients
|
|
|
|
Correlations rxy and ryz
|
|
Reliability of all
variables
|
rxz
|
0.10
|
0.20
|
0.30
|
0.40
|
0.50
|
0.60
|
0.70
|
0.80
|
|
0.90
|
0.10
|
0.10
|
0.20
|
0.30
|
0.40
|
0.50
|
0.60
|
0.70
|
0.80
|
|
0.90
|
0.40
|
0.08
|
0.15
|
0.23
|
0.31
|
0.38
|
0.46
|
0.54
|
0.62
|
|
0.90
|
0.70
|
0.06
|
0.13
|
0.19
|
0.25
|
0.31
|
0.38
|
0.44
|
0.50
|
|
|
|
|
|
|
|
|
|
|
|
|
0.80
|
0.10
|
0.11
|
0.22
|
0.33
|
0.44
|
0.56
|
0.67
|
0.78
|
0.89
|
|
0.80
|
0.40
|
0.08
|
0.17
|
0.25
|
0.33
|
0.42
|
0.50
|
0.58
|
0.67
|
|
0.80
|
0.70
|
0.07
|
0.13
|
0.20
|
0.27
|
0.33
|
0.40
|
0.47
|
0.53
|
|
|
|
|
|
|
|
|
|
|
|
|
0.70
|
0.10
|
0.13
|
0.25
|
0.38
|
0.50
|
0.63
|
0.75
|
0.88
|
---
|
|
0.70
|
0.40
|
0.09
|
0.18
|
0.27
|
0.36
|
0.45
|
0.55
|
0.64
|
0.73
|
|
0.70
|
0.70
|
0.07
|
0.14
|
0.21
|
0.29
|
0.36
|
0.43
|
0.50
|
0.57
|
|
|
|
|
|
|
|
|
|
|
|
|
0.60
|
0.10
|
0.14
|
0.29
|
0.43
|
0.57
|
0.71
|
0.86
|
---
|
---
|
|
0.60
|
0.40
|
0.10
|
0.20
|
0.30
|
0.40
|
0.50
|
0.60
|
0.70
|
0.80
|
|
0.60
|
0.70
|
0.08
|
0.15
|
0.23
|
0.31
|
0.38
|
0.46
|
0.54
|
0.62
|
|
Notes: Calculations in this table utilized Formula 4,
assumed all IVs had the same reliability estimate, assumed each IV had the same
relationship to the DV, and assumed each IV had the same variance in order to
simplify the example. Numbers reported represent corrected rxz. |
Reliability and
interactions in multiple regression
To
this point the discussion has been confined to the relatively simple issue of
the effects of low reliability, and correcting for low reliability, on simple
correlations and higher-order main effects (partial correlations, multiple
regression coefficients). However, many interesting hypotheses in the social
sciences involve curvilinear or interaction effects. Of course, poor
reliability of main effects is compounded dramatically when those effects are
used in cross-products, such as squared or cubed terms, or interaction terms.
Aiken and West (1996) present a good discussion on the issue. An illustration
of this effect is presented in Table 4.
As
Table 4 shows, even at relatively high reliabilities, the reliability of
cross-products is relatively weak. This, of course, has deleterious effects on
power and inference. According to Aiken and West (1996) there are two avenues
for dealing with this: correcting the correlation or covariance matrix for low
reliability, and then using the corrected matrix for the subsequent regression
analyses, which of course is subject to the same issues discussed above, or
using SEM to model the relationships in an error-free fashion.
|
Table 4: The
effects of reliability on cross-products in multiple regression
|
|
|
Correlation between X and Z
|
|
Reliability of X and Z
|
0.00
|
0.20
|
0.40
|
0.60
|
|
0.9
|
0.81
|
0.82
|
0.86
|
0.96
|
|
0.8
|
0.64
|
0.66
|
0.71
|
0.83
|
|
0.7
|
0.49
|
0.51
|
0.58
|
0.72
|
|
0.6
|
0.36
|
0.39
|
0.47
|
0.62
|
|
Note: These
calculations assume both variables are centered at 0, and assume both X and Z
have equal reliabilities. Numbers reported are cross-product reliabilities. |
Protecting against
overcorrecting during disattenuation
The
goal of disattenuation is to be simultaneously accurate (in estimating the
“true” relationships) and conservative in preventing overcorrecting.
Overcorrection serves to further our understanding no more than leaving
relationships attenuated.
There
are several scenarios that might lead to inappropriate inflation of estimates,
even to the point of impossible values. A substantial under-estimation of the
reliability of a variable would lead to substantial over-correction, and
potentially impossible values. This can happen when reliability estimates are
biased downward by heterogeneous scales, for example. Researchers need to seek
precision in reliability estimation in order to avoid this problem.
Given
accurate reliability estimates, however, it is possible that sampling error, a
well-placed outliers, or even suppressor variables could inflate relationships
artificially, and thus, when combined with correction for low reliability,
produce inappropriately high or impossible corrected values. In light of this,
I would suggest that researchers make sure they have checked for these issues
prior to attempting a correction of this nature (researchers should check for
these issues regularly anyway).
Other solutions to the
issue of measurement error
Fortunately,
as the field of measurement and statistics advances, other options to these
difficult issues emerge. One obvious solution to the problem posed by
measurement error is to use Structural Equation Modeling to estimate the
relationship between constructs (which can be theoretically error-free given
the right conditions), rather than utilizing our traditional methods of
assessing the relationship between measures. This eliminates the issue of over
or under-correction, which estimate of reliability to use, and so on. Given
the easy access to SEM software, and a proliferation of SEM manuals and texts,
it is more accessible to researchers now than ever before. Having said that,
SEM is still a complex process, and should not be undertaken without proper
training and mentoring (of course, that is true of all statistical procedures).
Another
emerging technology that can potentially address this issue is the use of Rasch
modeling. Rasch measurement utilizes a fundamentally different approach to measurement
than classical test theory, which many of us were trained in. Use of Rasch
measurement provides not only more sophisticated, and probably accurate,
measurement of constructs, but more sophisticated information on the
reliability of items and individual scores. Even an introductory treatise on
Rasch measurement is outside the limits of this paper, but individuals
interested in exploring more sophisticated measurement models are encouraged to
refer to Bond and Fox (2001) for an excellent primer.
An Example from
Educational Psychology
To
give a concrete example of how important this process might be as it applies to
our fields of inquiry, I will draw from a survey I and a couple graduate
students completed of the Educational Psychology literature from 1998 to 1999.
This survey consisted of recording all effects from all quantitative studies
published in the Journal of Educational Psychology during the years 1998-1999,
as well as ancillary information such as reported reliabilities.
Studies
from these years indicate a mean effect size (d) of 0.68, with a
standard deviation of 0.37. When these effect sizes are converted into simple
correlation coefficients via direct algebraic manipulation, d = .68 is
equivalent to r = .32. Effect sizes one standard deviation below and
above the mean equate to rs of .16 and .46, respectively.
From
the same review of the literature, where reliabilities (Cronbach’s a) are reported, the average reliability is a = .80, with a standard deviation of .10.
Table
5 contains the results of what would be the result for the field of Educational
Psychology in general if all studies in Educational Psychology disattenuated
their effects for low reliability (and if we assume reported reliabilities are
accurate). For example, while the average reported effect equates to a
correlation coefficient of r =.32 (accounting for 10% shared variance),
if corrected for average reliability in the field (a = .80) the better estimate of that effect is r =.40, (16%
shared variance, a 60% increase in variance accounted for.) These simple
numbers indicate that when reliability is low but still considered acceptable
by many (a = .70, one standard deviation below the average
reported alpha), the increase in variance accounted for can top 100%-- in this
case, our average effect of r = .32 is disattenuated to r = .46,
(shared variance of 21%). At minimum, when reliabilities are good, one
standard deviation above average (a = .90), the gains
in shared variance range around 30%- still a substantial increase.
|
Table 5: An
example of disattenuation of effects from Educational Psychology literature.
|
|
|
Small effect
( r= .16, r2 = .025, d =
.32)
|
Average effect
( r= .32, r2 = .10, d =.68)
|
Large effect
(r = .46, r2 = .21, d =
1.04)
|
|
Poor reliability
(a = .70)
|
r = .23
r2 = .052
d = .47
|
r = .46
r2 = .21
d = 1.04
|
r = .66
r2 = .43
d = 1.76
|
|
Average reliability
(a = .80)
|
r = .20
r2 = .040
d = .41
|
r = .40
r2 = .16
d = .87
|
r = .58
r2 = .33
d = 1.42
|
|
Above-average reliability
(a = .90)
|
r = .18
r2 = .032
d = .37
|
r = .36
r2 = .13
d = .77
|
r = .51
r2 = .26
d = 1.19
|

Summary, Caveats, and
Conclusions
If
the goal of research is to be able to provide the best estimate of an effect
within a population, and we know that many of our statistical procedures assume
perfectly reliable measurement, then we must assume that we are consistently
under-estimating population effect sizes, usually by a dramatic amount. Using
the field of Educational Psychology as an example, and using averages across
two years of high-quality studies, we can estimate that while the average
reported effect size is equivalent to r = .32, (10% variance accounted
for), once corrected for average reliability the average effect is equivalent
to r =.40, (16% variance accounted for). This means that the reported
numbers, not corrected for low reliability, under-estimate the actual
population effect sizes by 37.5%.
However,
there are some significant caveats to this argument. In order to disattenuate
relationships without risking over-correction you must have a good estimate of
reliability, preferably Cronbach’s alpha from a homogeneous scale. Second,
when disattenuating relationships, authors should report both original and
disattenuated estimates, and should explicitly explain what procedures were
used in the process of disattenuation. Third, when reliability estimates drop
below .70 authors should consider using different measures, or alternative
analytic techniques that do not carry the risk of over-correction, such as
latent variable modeling, or better measurement strategies such as Rasch
modeling.
Author Notes
Table
2 was published previously in Osborne and Waters (2002). I would like to
acknowledge the contributions of Thomas Knapp in challenging my assumptions and
thinking on this topic. I hope the paper is better because of his efforts.
References
Aiken, L. S., & West, S. G. (1996).
Multiple regression: Testing and interpreting interactions. Thousand Oaks, CA: Sage.
Bohrnstedt, G. W. (1983). Measurement.
In P. H. Rossi, J. D. Wright, & A. B. Anderson (Eds.) Handbook of Survey
Research. San Diego, CA: Academic
Press.
Bond, T. G., & Fox, C. M. (2001). Applying
the Rasch Model: Fundamental Measurement in the Human Sciences. Mahwah, NJ: Erlbaum.
Nunnally, J. C. (1978). Psychometric
Theory (2nd ed.). New
York: McGraw Hill.
Osborne, J. W., Christensen, W. R., & Gunter, J.
(April, 2001). Educational Psychology from a Statistician’s Perspective: A
Review of the Power and Goodness of Educational Psychology Research. Paper
presented at the national meeting of the American Education Research
Association (AERA), Seattle, WA.
Osborne, J. W., & Waters, E. (2002).
Four assumptions of multiple regression
that researchers should always test. Practical Assessment, Research, and
Evaluation, 8(2). [Available online at http://ericae.net/pare/getvn.asp?v=8&n=2
].
Pedhazur, E. J., (1997). Multiple
Regression in Behavioral Research (3rd ed.). Orlando, FL:Harcourt
Brace.
Jason
W. Osborne can be contacted via email at jason_osborne@ncsu.edu,
or via mail at: North Carolina State University, Campus Box
7801, Raleigh NC 27695-7801.
Sitemap 1 - Sitemap 2 - Sitemap 3 - Sitemap 4 - Sitemape 5 - Sitemap 6
|

