Cody Ding
University of Missouri - St. Louis

Studying change processes in education and the behavioral sciences has been of interest for a long time.  Researchers and practitioners in the behavioral sciences are concerned with questions about how individuals change over time (Willett & Sayer, 1994; Williamson, Appelbaum, & Epanchin, 1991).  That is, we are interested in the question of how individual change in certain attributes (for example, change of masculinity and femininity among adolescents) is related to selected characteristics of a person's background, family and peer environment, or training.  In recent years, the number of models utilized to address questions of this kind has increased substantially (e.g., Collins & Horn, 1991; Aber & McArdle, 1991). 

The focus of this paper is not to compare different methods in modeling growth curve. Rather, the current study is to propose a longitudinal profile analysis via Multidimensional Scaling (PAMS), called LPAMS model.  This is an exploratory approach to identify growth patterns in the data using Multidimensional Scaling, an alternative to more commonly used theory-based structural equations model approach (e.g., McArdle & Epstein, 1987). 

The longitudinal multidimensional scaling analysis described here is an exploratory technique.  There are several reasons for using the LPAMS model rather than more traditional approaches such as structural equations modeling.  First, the LPAMS model is most suitable for the situation in which the growth patterns are to be derived from the data, rather than specified by theory.  It requires no a priori hypotheses about the nature of the underlying growth patterns.  While a priori specification of a unidimensional growth pattern model is often feasible, the difficulty of specifying the growth patterns a priori increases as the number of growth curves increases.

Second, it provides estimates of latent growth pattern as well as estimates of individual growth parameters in the model (that is, growth rate estimates for each individuals), not simply summary statistics such as means, variances, and covariances.  If one wishes to study inter-individual differences in growth profiles, one may take the individual growth parameter estimates as a description of his or her entire growth pattern and subject those parameter estimates to multivariate analysis of variance or regression analysis. 

In a sense, LPAMS is similar to multilevel or hierarchical modeling in that it allows one to estimate both group level growth parameters and individual growth rate, where within-subject is considered level 1 model and between-subjects is considered level 2 model (Willett & Sayer, 1994).  After obtaining level 1 individual growth rate estimate and initial status estimate, one can examine between-group differences in these parameter estimates.  The differences between the LPAMS model and the commonly-used hierarchical linear model (HLM) are that: First, in HLM there is clustering of individuals within group and variables are measured at all available levels, thus combining variables from different levels in one statistical model, whereas in the LPAMS model one estimates within-individual change with respect to the latent change curves using MDS method and estimates between-individual variations via conventional ANOVA approach.  Second, they differ on some of the assumptions, which are discussed below.

Third, the assumptions are minimal.  The more traditional models suffer from complaints about the theoretical restrictions and lack of applicability of many standard linear models that assume the normal distribution (Nesselroade & Ford, 1987; Nesselroad & Cattell, 1989).  The LPAMS model allows for simultaneous estimation intra- and inter-individual growth processes without requirement of the multivariate normality of tests frequently employed.  It can be applied to the data that are not amenable to the common methods of analysis due to limitations imposed by the specific design of experiment, or theoretical assumptions about the nature of the phenomenon under study. 

Fourth, the LPAMS model is based on distance model (Borg & Groenen, 1997; Davison, 1983) rather than linear model.  Thus, it can be used to model data that are nonlinear in nature.  In LPAMS modeling, the growth patterns are examined, not just mean score change over time, which can usually be analyzed using a standard univariate or multivariate repeated-measures design.  This is especially the case when there may be more than one growth curves in the data and the LPAMS model can simultaneously identify these curves.     

As with any methodology, there are several limitations associated with this exploratory longitudinal MDS approach.  First, as with any exploratory approach, it is designed to identify patterns of growth underlying a set of data, not to test a priori hypotheses about patterns.  Therefore, it will often be most useful in the early stages of a research program in which little is known about the underlying growth patterns.  Second, while it requires no distributional assumptions about the observed variables, it does require equal error variances at each time period, which may not be realistic. 

In rest of the paper, the focus will be on discussing the multidimensional scaling (MDS) model underlying longitudinal profile analysis and on how the LPAMS model can be used for growth curve analysis.  Next, parameter estimation is considered.  The parameter estimation scheme involves obtaining an initial estimate of growth curve parameters, re-scaling them to facilitate interpretation in the context of growth curve analysis, and then estimating the individual growth parameters.

Longitudinal Profile Analysis via Multidimensional Scaling (LPAMS)

Longitudinal Profile Analysis via MDS Model

A multidimensional scaling (MDS) model produces a geometric or spatial representation of relationships between stimuli or individuals.  The goal is to produce a geometric representation of underlying individual or stimuli dimensions that fit the data based on spatial proximity between pairs of objects as a measure of their relatedness.  A classical MDS example used to identify latent stimuli dimensions is the research on the children’s cognitive reasoning of body parts (Jacobowitz, 1975).  In this study, children were presented with pairs of body parts.  They were asked to sort the body parts according to the functions of these parts.  MDS was used to model the nature of a child’s conception in the geometric space in which subjects locate their perceptions of the different body parts.  

This geometric representation of underlying stimuli can be extended to examining how a set of variables is patterned or configured in a space.  The research focus is on what typical patterns or configurations of variables actually exist in the population and how individuals differ with respect to these patterns.  This is what MDS profile analysis attempts to answer (e.g., Davison, Gasser, & Ding, 1996; Davison, Kuang, & Kim, 1999).  Figure 1 is an example of such a latent profile analysis of vocational interest profiles based on well-known hexagonal theory of vocational interest (Campbell & Hansen, 1985).   As can be seen from the figure, each interest variable is located along the two dimensions according to their scale values x_k(t), which quantify the relationships among the variables under inquiry.

Figure 1.  Latent profile patterns for vocational interests.

The above examples serve to demonstrate two applications of the MDS model.  One can build on these concepts and extend the model for longitudinal studies.  When the variable under the study is repeated at different occasions, however, the repeated variable is expected to be related to one other in the form of a particular developmental shape along the certain dimensions.  Therefore, one may conceptualize the magnitude of that variable as a function of characteristics of that person as well as time of measurement.  The MDS model used in such longitudinal data analysis is called longitudinal profile analysis via multidimensional scaling (LPAMS) model.  In this model, each growth curve dimension k represents an exemplar of a particular arrangement of scores of different time points, called a prototypical growth pattern or latent growth pattern, which is defined by the scale value x_k(t) estimates from the model. 

Longitudinal profile analysis via MDS model starts with the equation:

where m _p(t) is the score of person p at time t; x_k(t) is scale value estimates that reflect the location of a repeated variable at time t along the developmental curve k, leading to k^th unspecified longitudinal curve for all individuals; w_pk is an individual growth profile index that the person p attaches to the x_k(t), quantifying the degree to which each individual’s observed profiles resemble the several dimensions (patterns) indexed by the subscript k.  Each dimension k can be considered a growth trajectory, and each person’s individual growth profile is modeled as a linear combination of the K trajectories represented by dimensions; c_p is a level parameter or intercept estimate, and e_p(t) is an error term.

The point of the foregoing discussion is that a set of variables or a set of scores of a repeated variable can be configured in a multidimensional space according to their locations in k-spaces; a particular arrangement of scores based on their scale value estimates may form a latent pattern or growth curve.  This pattern does not indicate homogeneity of construct of a set of variables, as in factor analysis; rather it represents a psychological characteristic shape and level of the variable under inquiry.     

Graphically the concepts of k^th latent growth shape and an individual growth profile can be represented as that in Figure 2.

Figure 2.  The kth latent growth shape and an individual growth pattern.

The intercept or level parameter, c_p, can be defined in several ways, depending on how the origin of the MDS solution is set.  In longitudinal data analysis, for example, if one wishes to study growth curve, the zero point can be set to correspond with the scale value at the first time period (i.e., x_k(1) = 0 for all k), then c_p becomes the expected score under the model for person p at the initial time t = 1.  That is, in Equation 1, if x_k(1) = 0 for every k, then the model predicted data point at time 1 for person p, m_p(1)^¢ = S_k w_pk x_k(1) + c_p  reduces to m_p(1)¢ = c_p.  Given the importance of initial level in the literature on growth, researchers may wish to set the zero point along dimensions so that the intercept for person p can be interpreted as the model predicted estimate of initial level for person p. 

Estimating Parameters in the Model.         

The LPAMS model analysis begins by using MDS to obtain initial estimates of the scale values x_k(t) in the model of Equation 1.  Once the initial estimates are obtained, the zero point on each dimension can be re-scaled so that intercept or level parameter estimate can be interpreted as initial level.  Having set the origin of dimensions, the individual growth parameters in the model, c_p and w_pk, can then be estimated by regressing the raw data m_p(t) in row p onto the now-known scale value estimates, x_k(t). 

Assumptions   LPAMS analysis model is based on distance model.  The assumptions on which the LPAMS analysis is based are mostly restrictions to uniquely identify the MDS solution rather than assumptions that limit the fit of the model to the data.  The only assumptions of Equation 1 are that (1) the variance of the deviations about the model be equal at all occasions of measurement, i.e., (1/P)Σe_p(t)² = σ²(e) for all t and (2) the errors are independently distributed with mean zero.  Beyond these, the analysis requires no other distributional assumptions such as normality.  

Initial MDS Estimates of Scale Value x_k(t).  In an LPAMS analysis based on distance model, the analysis begins with a matrix containing a proximity measure defined over all possible pairs of stimuli.  In fact, the choice between using a distance measure and a correlation/covariance is not that important (Borg & Groenen, 1997).  In our case, the stimuli are time points, and the proximity measure for each possible pair of time points (t, t’) is a squared Euclidean distance measure, d_tt'², computed from the raw data as follows:

Table 1 shows the square root of squared Euclidean distance matrix thus computed based on reading achievement.  The distance coefficients indicates the degree to which the reading scores differ from each other over time.  The proximity module in many standard statistical packages (e.g. SAS, SPSS, SYSTAT) includes an option for the computation of squared Euclidean distance or Euclidean distance proximity measures defined over all possible pairs of variables. 

When proximity measures Equation 2 are submitted to an appropriate multidimensional scaling algorithm, the analysis should yield one dimension for each latent growth curve.  Since the objective of the LPAMS model analysis is to see if there are particular trend shapes in the data, whether they are linear curve, nonlinear curve, or time-series periodic curves, MDS estimation method would identify one or more such trend shapes when such curves exist in the data.  Thus, LPAMS model configures repeated data points in k-dimensions, and the scale value for time t along dimension k will provide an estimate of x_k(t) in the LPAMS model of Equation 1, with these estimates representing the prototypical growth patterns along the dimensions.     

Re-scaling the Origin of the Dimensions.   In most, if not all, MDS algorithms, the zero point along each dimension is set equal to the mean scale value along that dimension.  Consequently, if one employs commonly available MDS algorithms, the zero point along each dimension may not be set so as to yield the desired interpretation of the intercept parameter c_p.  After x*_k(t), the initial estimate of the scale value for time t along dimension k, is obtained, the zero point can be re-set so as to correspond with the location of the first time period simply by taking each initial estimate and subtracting x*_k(1).  That is, the final estimate of each scale value x_k(t) can be computed from the initial estimates according to the following formula: x_{k(t) =}  x*_k(t) – x*_k(1) for all k and t.  If the origin is thus re-set, each intercept parameter estimate (obtained below) can be interpreted as the initial level for person p.  Such change of the origin must take place before estimating the person parameters in the next step in order to obtain the desired interpretation of the intercept estimates.

Estimating Individual Differences Parameters.  Once the final scale values have been obtained, least squares estimates of the person parameters, c_p and w_pk, can be estimated through regression.  By treating m_p(t) as scores on a “criterion” variable and the scale values along each dimension as “predictor” scores, one can regress the criterion variable, the data m_p(t) in row p, onto the several predictor dimensions, x_k(t), to estimate the intercept c_p and the several growth profile index (also called slope or salience weight) w_pk for person p. 

Thus, LPAMS model analysis proceeds in three steps.  First, proximity measures are computed over all possible pairs of times according to Equation 2.  These proximity measures are analyzed using nonmetric MDS algorithms to yield estimates of the scale values x_k(t) in the  model.  In the second step, the zero point along each dimension is re-set, if necessary, so that the estimates of the intercept parameters will have the desired interpretation.  Finally, the individual growth parameters c_p and w_pk are estimated by regressing each person’s raw data onto the MDS scale values. 

A concrete example may elucidate the LPAMS model analysis.  The SAS codes are provided in the appendix so that reader can carry out the analysis.  The data were from student reading achievement over a four-year span.  Like many in the literature, it includes only one latent growth pattern, i.e., only one dimension.  It should be noted that this was a coincident in that there were only four repeated measures available over four years for the current study.  In fact, more data points are desirable in such applications so that different growth curves can be studied.   

LPAMS Growth Profile Analysis on Reading Achievement Test

To illustrate the use of the LPAMS model for exploratory growth profile analysis, a data set containing four waves of data was used.  The data was obtained from a sample of 705 elementary and middle school students at a school district in a Southwest state.  These students consisted of 2 cohorts.  Grade 3 cohort students were in 3^rd grade at the first time of measurement and grade 5 cohort students were in 5^th grade at the first time of testing.  The same students were followed for four years.  For grade 3 cohort, each students completed the Stanford Reading Test---Ninth edition at each grade (i.e., at 3^rd, 4^th, 5^th, and 6^th grades).  Similarly, grade 5 cohort students were repeatedly assessed using the same test at 5^th, 6^th, 7^th, and 8^th grade.  The test was used by the school district to measure students' academic progress over the years.  The scores were reported as scaled scores for each student across these four waves of data collection. 

Table 2 shows the means and standard deviations of the reading scores for these two cohorts.  These statistics are based on 705 students who had complete data on all four occasions of measurement.  Inspection of the table indicated that students did seem to progress in their reading achievement over the years, with grade 3 cohort students showing decreased variations over time, indicating on average students were less scattered in their reading scores. 

Exploratory LPAMS Analysis of Growth Profiles

Exploratory longitudinal profile analysis via multidimensional scaling (LPAMS) started with estimating scale values presented in Equation 1.  As mentioned above, time is specified as the latent dimension along which individuals vary with regard to the growth/decline curve.  In applying this model, the reading score is considered a repeatedly measured variable on a time dimension along which individual change patterns are of interest.  Since the analysis is exploratory, no specification of a particular growth/decline profile is necessary.  The growth patterns are to be derived from the observed data.

Estimating scale values   In the LPAMS growth analysis, the squared Euclidean distance was first computed from raw scores on reading tests based on Equation 2, which were then used as input for nonmetric MDS analysis using SAS.

Next, initial scale values, x_k(t),  were estimated using nonmetric MDS procedures and one dimensional solution was identified.  These scale values reflect growth rates over a four year span.  As a rule, five or more variables are needed to define a dimension (Davison, 1983).  Since there were only four repeatedly measured variables in the current data, no more than one trajectory dimension (i.e., one growth pattern) seemed to be justified.  The adequacy of a one dimensional MDS solution was verified by the MDS fit index, STRESS-1 formula (Kruskal, 1964).  The STRESS-1 value was zero (S₁ = 0.00), indicating that the observed data points fit the one-dimensional MDS model well. 

The estimates of LPAMS growth curve values (i.e., scale values of the repeated variable) are presented in Table 3.  The scale values in Table 3 are the final estimates obtained by re-scaling the initial estimates in such a way that the zero point corresponds to the scale value of time 1 so that intercept or level estimate indicate the initial level.  To facilitate the presentation of the scale values, they were scaled to have a mean of 5 and a standard deviation of 2.  This was a simple linear transformation that did not affect the interpretation of the scale values.  Growth rates in percentage for each of the three time intervals were also shown in the table.  These growth rates remained the same regardless of the translation of the scale values.

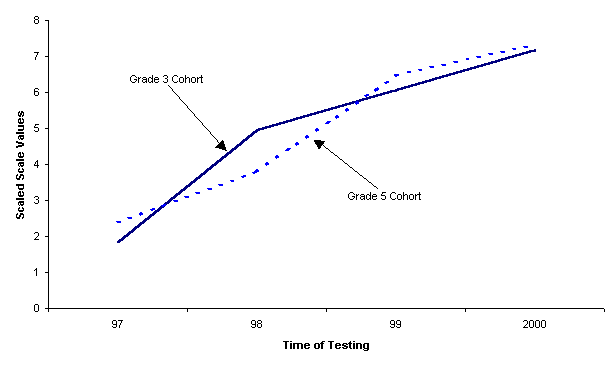
Figure 3 shows the latent growth pattern based on the final growth scale values.  The dimension scale values depict the latent growth pattern in terms of three line segments.  Each segment covers one time interval: year 97 to 98, year 98 to 99, and year 99 to 2000.  Differences in growth rate over the several time intervals are represented by the slopes of the line segments for those intervals.   As can be seen in Figure 3, for grade 3 cohort, the pattern showed the greatest growth rate from 3^rd grade to 4^th grade.  In this pattern, 58% of the growth occurred over this first interval.  The growth rate slowed down from 4^th grade to 6^th grade.  In this pattern, 21% of the growth occurred from 4^th to 5^th grade and 21% from 5^th to 6^th grade.  For grade 5 cohort, the growth rate showed the slow growth rate from 5^th grade to 6^th grade, with 29% of growth occurring over this first interval.  The greatest growth rate occurred from 6^th to 7^th grade.  In this pattern, 54% growth occurred.  In the last time interval, growth rate slowed down again, with 17% growth in reading achievement.

Figure 3.   Latent growth pattern in reading achievement.

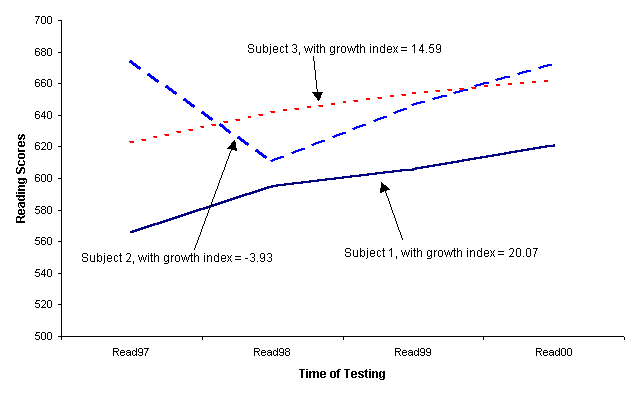
Estimating individual growth parameters   The last step in the LPAMS growth profile analysis was to estimate individual growth parameters c_p and w_pk through regression.  c_p is the intercept for person p, and it can be interpreted as the model predicted estimate of initial level for person p;  that is,  c_p becomes the expected score under the model for person p at the initial time (t = 1).  The w_pk are the growth profile index, quantifying the p^th  individual with regard to the k^th   latent growth pattern and mapping the observed data onto growth trajectory represented by the dimension.  If the model fits the data, then for any given interval, growth is fastest for individuals with higher values of w_pk.  In Figure 4, subject 1 had a larger growth profile index than (w = 20.07) did subject 3 (w = 14.59), with subject 1 showing faster growth than subject 3, although both subjects resembled the latent growth profile.  Subject 2 had slowest growth (-3.93) over time.

Figure 4.   Individual growth curve in reading achievement.

In the current data, the average of the growth profile index was 19.85, with a standard deviation of 9.01 for grade 3 cohort, and was 16.50, with a standard deviation of 8.08 for grade 5 cohort.  This indicated that, on average, students had made gains in reading scores over the years, with certain individual variation in growth profiles.  The correlation between the intercept c_p (i.e., initial status) and the profile correspondence index w_pk was -.59 and -.29 for each cohort respectively, indicating that students who had high initial reading scores tended to make less gain in achievement over the four year period. 

Conclusion

In recent years, latent growth curve modeling has been widely used in longitudinal research.  Some authors (e.g., McArdle & Epstein, 1987; Meredith & Tisak, 1990; Muthen, 1991) have demonstrated how concepts of individual growth modeling can be accommodated within the framework of covariance structure analysis.  In this paper, an exploratory growth profile analysis was proposed.  The approach uses MDS model based on squared Euclidean distance measures of proximity defined over pairs of time periods to model growth curve in the data.  Such longitudinal profile analysis by means of MDS can be used to study individual and group patterns of longitudinal change in an exploratory fashion.  Latent growth rates are reflected in the estimates of scale values from MDS geometric solutions, which could simultaneously accommodate one or more growth curves in the data.  Individual growth profile index is also estimated from the model so that one could directly study the inter-individual differences with respect to growth.

One drawback of the current study is that there are only 4 longitudinal data points available due to the difficult of obtaining the longitudinal data with more time points.  This limits the demonstration of using the LPAMS model to identify different growth curves in the data, which is one of the major insights that can be made from the analysis.  Readers are encouraged to try out this technique using their own data, preferably with eight or more time points.

References

Aber, M. S., & McArdle, J. J.  (1991).  Latent growth curve approach to modeling the development of competence.  In M. Chandler & M. Chapman (Eds.), Criteria for competence: Controversies in the conceptualization and assessment of children's abilities (pp. 231-258).  Mahwah, NJ: Lawrence Erlbaum Associates.

Borg, I, & Groenen, P.  (1997).  Modern Multidimensional Scaling:  Theory and applications.  New York: Springer.

Campbell, D. P., & Hansen, J. C.  (1985).  Strong-Campbell Interest Inventory.  Palo Alto, Stanford University Press.

Collins, L. M., & Horn, J. L.  (1991). Best methods for the analysis of change:  Recent advance, unanswered questions, future directions.  Washington, DC:  American Psychological Association.

Davison, M. L., Gasser, M., & Ding, S. (1996).  Identifying major profile patterns in a population: An exploratory study of WAIS and GATB patterns.  Psychological Assessment, 8, 26 – 31.

Davison, M. L., Kuang, H., & Kim, S.  (1999).  The structure of ability profile patterns: A multidimensional scaling perspective on the structure of intellect.  In P. L. Ackerman, P. C. Kyllonen, & R.D. Roberts (Eds.).  Learning and individual differences: Process, trait, and content determinants (pp. 187 – 204).  Washington, D. C.: APA Books.

Kruskal, J. B.  (1964). Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis.  Psychometrika, 29, 1-27.

Jacobowitz, D.  (1975).  The acquisition of semantic structures.  Unpublished doctoral dissertation, University of North Carolina at Chapel Hill.

McArdle, J. J., & Epstein, D.  (1987).  Latent growth curves within developmental structural equation models.  Child Development, 58, 110-133.

Meredith, W.,  & Tisak, J.  (1990).  Latent curve analysis.  Psychometrika, 55, 107-122.

Muthen, B. O.  (1991).  Analysis of longitudinal data using latent variable models with varying parameters.  In  L. M. Collins & J. L. Horn (Eds.), Best methods for the analysis of change:  Recent advance, unanswered questions, future directions.  Washington, DC:  American Psychological Association.

Nesselroade, J. R., & Cattell, R. B.  (1989).  Handbook of multivariate experimental psychology.  New York: Plenum Press.

Nesselroade, J. R., & Ford, D.  (1987).  Putting the framework to work: Methodological implications of the systems framework.  In D. Ford (Ed.), Human as self-constructing living systems: a developmental perspective on behavior and personality (pp. 47-79).  Hillsdale, NJ: Lawrence Erlbaum.

Willett, J. B., & Sayer, A. G.  (1994).  Using covariance structure analysis to detect correlates and predictors of individual change over time.  Psychological Bulletin, 116, 363-381.

Williamson, G. L., Appelbaum, M., & Epanchin, A.  (1991).  Longitudinal analyses of academic achievement.  Journal of Educational Measurement, 28, 61-76.

Appendix:  SAS Codes for Performing the LPAMS Analysis

%MACRO GROWTH (data =, var =, dim =, dimname= , pout= , subid = );

DATA trsf1 (Keep=&var);

set &data;

PROC TRANSPOSE DATA=trsf1 OUT=out;

var &var;

RUN;

%INCLUDE  'C:\program files\SAS institute\sas\v8\STAT\SAMPLE\xmacro.SAS';

%INCLUDE  'C:\program files\SAS institute\sas\v8\STAT\SAMPLE\DISTnew.SAS';

%INCLUDE  'C:\program files\SAS institute\sas\v8\STAT\SAMPLE\stdize.SAS';

%DISTANCE ( DATA=out, METHOD=EUCLID, id=_name_, OUT=dis );

RUN;

PROC PRINT data=dis; RUN;

/*MDS analysis*/

PROC MDS DATA=dis CONDITION=matrix  SHAPE=Triangle  LEVEL=ordinal

     COEF=i  FORMULA=1  FIT=1  DIMENSION= &dim  PFINAL

     OUT=scale_value  OUTRES=cordres

     ;

TITLE "Nonmetric MDS Growth Scale Values";

TITLE ‘   ‘;

RUN;

/*Re-scale and Estimate C and W*/

DATA profile (KEEP= &dimname);

SET scale_value (FIRSTOBS=2 ); 

PROC PRINT data=profile;

run;

PROC IML;

USE &data VAR{&var}; /*use original raw score variables*/

READ all INTO M ;

USE profile VAR{&dimname}; /*Read in initial scale values*/

READ ALL INTO X;

X = (X - X[1,1])* -1;

  /*Re-set the origin of the initial scale value and make them all positive */

Print X;

Print "This is final re-scaled estimates of growth scale values";

/*computes the weights and level parameters */

START w;

R=NROW(x);

COL=J(r,1,1);

X1=X||COL;

M1=inv(X1`*X1);  

M2=M*X1;

TW=M2*M1;

FINISH W;

RUN w;

/*computes the fit measure for each subject*/

START fit;

M1 = tw * x1`;

K = ncol(m);

R = nrow(m);

COL = j(1,k,1);

M1RSUM = m1-((m1[,+]*col)/k );

PVAR = (m1rsum##2)*col`;

MRSUM = m - ((m[,+] * col)/k);

VAR = (mrsum##2)*col`;

COL= pvar/var;

FINISH fit;

run fit;

/*Merge weights and level parameters with the fit measures */

WL=tw||col;

/*Get subject id from original data for merging dataset*/

use &data Var{&subid};

read all into id;

WL = id||WL;

MATTRIB WL COLNAME = ({&subid &DIMNAME LEVEL FIT});

CREATE &pout var{&subid &dimname level fit};

APPEND from WL;

SHOW DATASETS;

SHOW CONTENTS;

QUIT;

%MEND;

%GROWTH   /*user need to change these specifications based on their data*/

(data = work.g3,

 var = read97 read98 read99 read00,

 dim = 1, dimname=dim1 ,

 pout = wldata, subid = id  );